L’articolo affronta la questione della conflittualità nell’ambito delle organizzazioni proponendo la teoria dei giochi come possibile strumento di risoluzione. La riflessione qui presentata e le conclusioni cui si perviene si fondano sulla distinzione dei giochi a somma zero, definiti a priori non cooperativi, e quelli a somma diversa da zero (o somma positiva), che prevedono l‘adozione di strategie competitive, conflittuali o cooperative. Quando non è possibile conoscere a priori le modalità di svolgimento del gioco, e quindi la strategia vincente, il gioco diventa un dilemma, e ciò si può riscontrare nelle organizzazioni. La riconduzione al dilemma consente di utilizzare il c.d. “gioco dei falchi e delle colombe”, proposto dal biologo evoluzionista Smith, per contestualizzare le possibili soluzioni alla conflittualità in ambito aziendale.
Introduzione
La manifestazione fenomenologica del conflitto nei contesti organizzativi prende forma quando sussiste disaccordo, tensione o altre difficoltà tra due o più parti. Esso può insorgere nelle dinamiche interattive, tra singoli individui o tra gruppi di persone, all’interno della medesima organizzazione ed è essenzialmente dovuto alla percezione di una delle parti che i propri obiettivi e interessi siano contrastati dall’altra. In questa sede avanziamo l’ipotesi di non considerare il conflitto come un requisito statico bensì come una condizione strutturale, in quanto l’organizzazione non rappresenta un sistema cooperativo minacciato occasionalmente dal conflitto, ma un insieme articolato in condizione naturale di conflitto dinamico. Un’interpretazione che richiama l’approccio dialettico, di carattere strutturalista, in quanto stabilisce che nella relazione “tra sé e l’altro da sé[1]” il conflitto assume un significato di ineluttabilità. Una concezione in antitesi rispetto alla prospettiva dello Scientific Management[2], secondo il quale, il conflitto rappresenta una deviazione potenzialmente pericolosa, con conseguenze distruttive e disfunzionali all’interno di strutture organizzative normate che dovrebbero preservare l’ordine e l’efficienza. Il nostro interesse riguarda la fase della risoluzione del conflitto, il quale può avvenire in diversi modi. Le parti possono, ad esempio, arrivare a un accordo sui differenti stati del mondo, su come risolvere le difficoltà e le divergenze, facendo ricorso al confronto diretto, a una terza parte (ad es. il referente gerarchico) o mediante l’utilizzo dell’impianto metodologico della teoria dei giochi[3]. Quest’ultima rappresenta una branca della matematica applicata che si occupa principalmente dell’analisi del processo decisionale, tenendo presente che si intendono per giochi situazioni nelle quali i giocatori sono agenti razionali e devono assumere delle decisioni strategiche, considerando in altre parole le azioni e le reazioni degli altri partecipanti. L’obiettivo teorico consiste nell’impostare dei giochi interattivi, per la risoluzione dei conflitti, tra diversi individui: nello specifico sia dei giochi competitivi c.d. a somma zero, dove le vincite di un partecipante equivalgono sempre alle perdite dell’altro, che giochi cooperativi c.d. a somma diversa da zero dove le vincite di una parte non debbono corrispondere necessariamente alla sconfitta dell’avversario. Gli elementi strutturali che caratterizzano qualsiasi gioco, inteso come qualsiasi situazione di interazione strategica, sono rispettivamente: i giocatori, le strategie a loro disposizione e i payoff – i c.d. guadagni dei giocatori – associati a tutte le possibili combinazioni di strategie e/o risultati del gioco. Un‘altra condizione fondamentale riguarda l’ipotesi di giochi in cui le due parti devono decidere simultaneamente la propria strategia, infatti ogni giocatore conoscerà a priori soltanto i payoff dell’avversario, ma non la sua scelta effettiva dal momento che sussiste una condizione di asimmetria informativa tra i diversi giocatori.
Giochi a somma positiva e dilemmi
Nell’ambito del presente lavoro intendiamo focalizzare l’attenzione, esclusivamente, nei confronti di quei giochi, definiti a somma positiva, in cui la cooperazione può portare benefici a tutte le parti, tale presupposto comporta inevitabilmente l’introduzione di elementi vincolati alla comunicazione interna e alla fiducia reciproca, ma anche alla minaccia, qualora gli accordi stabiliti tra i partecipanti non vengano rispettati. In questi giochi si viene a configurare un conflitto parziale, dove gli individui agiscono influenzati simultaneamente da due tendenze parallele e antitetiche: la tendenza associativa, che porta alla socializzazione; quella dissociativa, che consolida l’atteggiamento individualistico delle persone. Pertanto, ogni relazione tra individui e gruppi di persone è la conseguenza del processo dinamico tra queste due opposte tendenze[4]. Possiamo distinguere, nell’interazione dei giochi a somma diversa da zero, la contemporanea presenza sia delle strategie competitive – non cooperative – che quelle cooperative. Quindi le decisioni che verranno prese dai giocatori presentano una tensione psicologica tra l’adozione di una strategia competitiva, finalizzata al perseguimento e alla massimizzazione dei propri interessi individuali, e quella di intraprendere una strategia di cooperazione con l’altro giocatore al fine di rendere sostenibile l’equilibrio del gioco ripetuto[5] nel corso del tempo.
| Giochi a somma zero | Strategia competitiva; assenza totale di collaborazione tra gli individui | Obiettivo: esiste solo la strategia competitiva/dominante |
| Giochi a somma diversa da zero | Presenza della strategia competitiva e cooperativa | Obiettivo: strategia dominante e cooperativa. Area del dilemma |
Tabella n. 1 – I differenti giochi e le relative strategie
In tale contesto prende forma il seguente interrogativo: quali saranno le decisioni di ogni giocatore? Dalla nostra analisi si profila quello che viene definito un dilemma, in quanto tutte le parti possono partecipare al gioco mediante una strategia cooperativa o competitiva ma non è possibile conoscere a priori quale decisione causerà maggiori benefici, dato che tutto dipende dalla decisione dell’avversario. In generale, la strategia cooperativa favorirà entrambi le parti rappresentando una situazione di first best per la risoluzione del conflitto, mentre il confronto interpersonale potrebbe verificare un risultato deludente per i giocatori. È evidente che se fossero presenti solo queste due possibilità verrebbe meno l’esistenza del dilemma ma se uno dei partecipanti intende cooperare mentre l’altro persegue la competizione, quest’ultimo maturerà i benefici che saranno maggiori di quelli ottenuti con la collaborazione: questa condizione rende evidente l’esistenza del dilemma. La complessità della teoria dei giochi fa sì che si debbano sistematizzare aspetti tipicamente matematici con altri di carattere psicologico ed anche morale, cioè di natura comportamentale, per cui i payoff non assumeranno soltanto il significato aritmetico di soluzione del problema: tali soluzioni si possono interpretare come delle possibilità che dipenderanno dalle decisioni dei contendenti.
Giochi a somma positiva e problema dell’opportunismo
A tal proposito vogliamo descrivere alcuni esempi di giochi a somma positiva, in relazione al problema dell’opportunismo tra le parti, nell’ambito di un contesto organizzativo, dove si possono adottare sia le strategie competitive finalizzate al perseguimento dell’interesse personale del giocatore che le strategie di cooperazione tra le parti. Queste tipologie di giochi si presentano più frequentemente nelle realtà organizzative dal momento che rilevano in modo più veritiero le situazioni conflittuali, espressione di una combinazione tra comportamenti cooperativi e competitivi. In un ipotetico scenario organizzativo, fortemente semplificato, possiamo immaginare la presenza di due individui, A e B, dove il soggetto A risulta essere un altruista che è sempre predisposto ad assumere un comportamento collaborativo con gli altri mentre B appare un egoista attivo principalmente verso il proprio tornaconto, i quali devono confrontarsi per la realizzazione di determinate attività economiche condivise all’interno dell’organizzazione. In tale contesto ogni decisione riguarderà l’interazione strategica tra i due individui, i quali possono decidere di adottare o un comportamento di cooperazione, ossia una condotta corretta nei confronti dell’altro altrimenti un comportamento competitivo, cioè finalizzato all’inganno. La tabella n. 2 mette in evidenza come i payoff ottenuti per entrambi gli individui (A e B) dipendono dalla specifica combinazione di comportamenti che risulta dalla loro scelta. In particolare, la struttura dei payoff della tabella si richiama perfettamente al modello di gioco conosciuto come il “dilemma del prigioniero[6]”. Possiamo constatare come i due individui sono in grado di realizzare dei guadagni più elevati mediante l’adozione di un comportamento non cooperativo, a prescindere dal comportamento dell’altro. Infatti, se A ipotizza che B assumerà un comportamento egoistico, sarà incentivato a sua volta a non collaborare, sia pure al fine di preservare il proprio status quo. In questa situazione di conflitto tra le parti si manifesta per gli individui la possibilità di scelta mediante l’adozione di una strategia dominante: quella che permette di realizzare i migliori risultati indipendentemente dalla strategia scelta dall’avversario. In questo gioco la strategia dominante risulta essere quella di non cooperare con l’altro individuo per la realizzazione del compito comune. Dall’analisi della tabella n.3 si comprende come, qualsiasi sia la scelta del soggetto A, l’individuo B otterrà sempre un guadagno maggiore perseguendo la strategia dominante, infatti:
- se A decidesse di non collaborare, il suo guadagno risulterebbe pari a 3 unità, il medesimo anche per B che adotta razionalmente la strategia dominante, e non pari a zero come nell’ipotesi in cui B avesse cooperato;
- Se A decidesse di collaborare, il suo guadagno risulta pari a 0 unità mentre per l’individuo B risulterebbe pari a 10 unità, sarà di conseguenza il soggetto A a sostenere per intero il costo e la fatica per la realizzazione dell’attività economica comune.
Naturalmente la struttura dei guadagni si presenta uguale per entrambi i giocatori, di conseguenza anche per A conviene non cooperare, adottando la strategia dominante, qualunque sia la scelta posta in essere da parte di B. In una situazione di conflitto quando tutti i giocatori perseguono un comportamento competitivo, e quindi egoistico, finalizzato al perseguimento del proprio interesse individuale si ritrovano inevitabilmente in una situazione peggiore rispetto al caso in cui avessero limitato la propria libertà d’azione: dal momento che non cooperano guadagnano 3 unità un livello inferiore rispetto al valore di 5 unità realizzato nel caso in cui il loro comportamento fosse stato in qualche modo reciprocamente vincolato tramite un accordo. Certamente il problema della mancanza di cooperazione tra le parti dipende dal fatto che i due individui non manifestano alcuna forma di fiducia. La semplice promessa di cooperare non modifica la struttura dei payoff tra i giocatori, anche se uno dei due individui avesse promesso di cooperare, l’altro beneficerebbe ancora dall’assumere un comportamento opportunistico, massimizzando il suo guadagno, specialmente quando sappiamo a priori che il gioco si ripeterà una sola volta e non si andrà incontro a delle sanzioni. Al contrario, come fu teorizzato dal R. Axelrod[7] con la strategia del c.d. “colpo su colpo” quando il gioco si ripete con maggiore frequenza, è possibile impostare delle strategie sulle interazioni precedenti, ponendo come fondamento la reciprocità. Infatti, si inizia il gioco cooperando e successivamente si dovrebbe ripetere quanto ha deciso l’avversario nella giocata precedente: se queste decisioni vengono rispettate, i partecipanti riconoscono chi ha cooperato e possono adottare delle azioni discriminatorie nei confronti degli individui che hanno disertato l’accordo.

Tabella n. 3 – La matrice dei guadagni monetari tra due individui nel caso di un compito in comune
Un ulteriore estensione del gioco, vincolato al problema dell’opportunismo, fa riferimento all’aumento della complessità del gioco medesimo, un’ipotetica situazione in cui nel contesto organizzativo non siano presenti soli due individui che giocano, A e B, ma un’intera popolazione di potenziali giocatori. Avremo di conseguenza coppie di individui che si associano per lo svolgimento di un compito comune sempre in relazione alla medesima struttura dei payoff e delle differenti strategie comportamentali a disposizione dei giocatori; con riferimento alla tabella n.4, la quale, definisce la presenza di due gruppi, rispettivamente Alfa e Beta, che partecipano al gioco invece di due soli individui. in relazione al concetto di popolazione, intendiamo il numero complessivo di individui che lavorano e collaborano all’interno di una data organizzazione, e che quindi possono appartenere ad uno dei due gruppi appena enunciati.

Tabella n. 4 – La matrice dei guadagni monetari tra due gruppi nel caso di un compito in comune
Tutti gli individui appartenenti all’organizzazione possono essere suddivisi, principalmente, in due gruppi: quello degli altruisti, si tratta di coloro che per ragioni dovute ad un forte condizionamento socioculturale, hanno maturato un sentimento morale particolarmente favorevole alla cooperazione e il gruppo degli egoisti, i quali sono predisposti esclusivamente all’adozione di comportamenti non cooperativi. Secondo questo modello comportamentale il gruppo degli altruisti rinunciano a priori alla possibilità di ingannare il prossimo anche quando non sussiste la possibilità di essere riconosciuti da parte degli altri individui. Questo comportamento li espone ad un elevato rischio dal momento che interagendo con un individuo egoista andrebbero in contro ad una perdita certa. Il gruppo degli egoisti, al contrario, che adottano senza soluzione di continuità la strategia dominante saranno in grado di massimizzare sempre i loro guadagni. L’interesse per il presente gioco, vincolato al problema della conflittualità potenziale tra le parti (in analogia al noto gioco dei falchi e delle colombe[8]), è finalizzato a stabilire cosa accadrà quando individui appartenenti a questi due gruppi si confrontano in un gioco ad interazione strategica nell’ambito di un dato contesto organizzativo. La soluzione dipende principalmente dal livello di complessità con cui è possibile distinguere le due tipologie di individui. In particolare, possiamo analizzare le due seguenti situazioni:
- Quella in cui non è possibile riconoscere, nella popolazione oggetto dell’indagine, gli individui altruisti da quelli egoisti. In questa situazione entrambi gli individui, sia gli altruisti che gli egoisti, apparentemente sono uguali e non esiste alcun criterio in grado di individuare la loro appartenenza ad uno dei due gruppi. In questa situazione tutti gli individui entreranno in contatto in modo casuale, chiaramente gli altruisti preferiranno interagire tra di loro ma non hanno alcuna possibilità di scelta. La struttura dei guadagni attesi di entrambi le parti, altruisti e egoisti, è funzione della probabilità di interagire con un altruista che a sua volta dipende dalla frazione di costoro all’interno della popolazione complessiva che partecipa al gioco. Possiamo stabilire che Px è la parte della popolazione rappresentativa degli individui altruisti quindi se uno di questi decidesse di cooperare con un individuo scelto casualmente, la probabilità che tale individuo sia collaborativo sarà Px mentre quella di trovare un opportunista equivale a 1-Px. Siccome un altruista, quando interagisce con individui dello stesso gruppo, presenta un guadagno di 5 unità, mentre con un individuo egoista ha un guadagno pari a zero, il guadagno atteso di ogni cooperatore è pari a:
Px = Px × 5 + [1-Px] × 0 = 5Px
L’analisi di questo gioca considerato come una metafora di una lotta per la sopravvivenza, in cui non è possibile riconoscere a priori a quale gruppo appartengono gli individui, rileva un dato fondamentale, quello per cui ogni persona si “riproduce” in proporzione ai propri guadagni medi: coloro che vantano dei guadagni più elevati potranno investire maggiori risorse per sviluppare famiglie più numerose. Se il gruppo degli egoisti presentano sempre dei guadagni più elevati di conseguenza la loro quota nella popolazione crescerà nel tempo. Gli altruisti, viceversa, anche se dovessero rappresentare fin dall’inizio la quasi totalità della popolazione andrebbero incontro alla loro estinzione in ragione dei più bassi payoff medi. In definitiva quando nel gioco si verifica l’impossibilità di riconoscere gli altruisti dagli egoisti allora risulta difficoltosa qualsiasi forma di cooperazione tra gli individui.
- Quella in cui è possibile riconoscere, nella popolazione oggetto dell’indagine, gli individui altruisti rispetto a quelli egoisti. In questa seconda situazione, semplificando le considerazioni di natura psicologica, con l’introduzione di un’emozione come l’empatia, si assume che possa favorire forme di cooperazione tra gli individui, e che la suddetta emozione presenti dei sintomi facilmente osservabili. Per gli individui egoisti, naturalmente, si rileva l’assenza totale dei suddetti sintomi e, pur tentando di avviare un processo di imitazione non vi riescono affatto. Se gli altruisti interagiscono in una condizione di simmetria informativa, in quanto possono sempre riconoscersi mediante un segnale comportamentale e relazionarsi tra di loro, allora possono ottenere un guadagno pari a 5 unità con riferimento alla tabella n.4. Si tratta di un risultato certo e non probabilistico in quanto nessun individuo altruistico vorrà interagire con un opportunista. Gli egoisti, al contrario, saranno obbligati a relazionarsi con gli individui del medesimo gruppo, e quindi il loro guadagno sarà inferiore cioè pari a 3 unità. In questa situazione la struttura dei payoff è perfettamente conoscibile a priori, i guadagni non dipendono più dalla numerosità degli altruisti all’interno della popolazione, in quanto non sono presenti elementi di incertezza legati alle dinamiche interattive tra gli individui. In questo gioco, al contrario del precedente, i guadagni medi più elevati da parte degli individui altruisti permetterà loro di sviluppare nuclei familiari più numerosi con la conseguenza che nel corso del tempo si vedrà accrescere la loro quota all’interno della popolazione complessiva. In definitiva, quando il gioco permette di riconoscere gli individui altruisti allora saranno gli egoisti in via di estinzione.
Il dilemma noto come il gioco “dei falchi e delle colombe”
In questo lavoro intendiamo analizzare il funzionamento e la logica del gioco dei falchi e delle colombe concepito, dall’illustre biologo evoluzionista John Maynard Smith[9], nell’ambito dei suoi approfondimenti nei modelli matematici e con particolare interesse alla teoria dei giochi per i suoi studi sull’evoluzione della specie. Gli animali che appartengono alla medesima specie ingaggiano costantemente dei combattimenti tra di loro, vuoi per il cibo o per il territorio e in particolare competono per il potere e per la riproduzione sessuale. Nel corso del tempo, la scienza biologica ha definito come convenzionali quei combattimenti che ricorrono frequentemente in natura e sono produttivi per il genere stesso. Dobbiamo partire dal presupposto che il processo di selezione naturale riguarda, principalmente, popolazioni o gruppi di specie ma spesso l’azione del singolo può contribuire a generare dei risultati inaspettati sul piano evolutivo. Le conflittualità che possono scaturire dalle lotte per la sopravvivenza, tra i membri della propria specie, sono il prodotto di modalità comportamentali differenti e devianti rispetto ad una tendenza normalizzata e che possono concludersi in cambiamenti significativi dal punto di vista genetico. Secondo l’approccio metodologico di Smith il combattimento di natura convenzionale, nell’ottica della selezione individuale, può sostanzialmente provocare due atteggiamenti distinti: quello di agire come un falco o come una colomba.
Per semplificare la nostra analisi, contestualizzando il gioco in un’ottica aziendale, consideriamo un’impresa composta di manager che presentano le medesime competenze tecniche ma differiscono sostanzialmente per la loro preferenza per il comportamento aggressivo, ossia di individui fortemente competitivi rispetto all’acquisizione di risorse economiche a disposizione dell’impresa.
Nello specifico avremo una tipologia di manager che definiremo la categoria dei “falchi[10]”, in quanto presentano una forte propensione all’aggressività, mentre gli altri verranno denominati la categoria delle “colombe[11]” visto la loro attitudine all’adozione di comportamenti non aggressivi – di base predisposti alla ricerca della collaborazione. La suddetta terminologia viene impiegata, nel senso metaforico del termine, al fine di delineare i membri della stessa specie animale con una differente predisposizione all’aggressività. La partecipazione di un individuo ad una delle due categorie, presenta un certo interesse, solo se quest’ultimo entra in una condizione di conflittualità con altri membri della popolazione al fine di acquisire le risorse rilevanti per la crescita dei suoi payoff (ad es. gestione dei budget aziendali, scelta dei team di progetto, etc.). Possiamo assumere la strategia del MF finalizzata al governo delle risorse aziendali, in presenza di un gioco a somma zero dove il guadagno di un individuo corrisponde sempre alla perdita dell’altro, viceversa la strategia della MC consiste nel rinunciare alla competizione per il possesso delle risorse.
A tal proposito ci si pone il seguente interrogativo: se queste due tipologie di individui si trovano in competizione tra di loro, per il presidio delle risorse, quale dei due dovrebbe riuscire vincente? In prima istanza risulterebbe razionale assumere come determinante la categoria dei falchi, in quanto risolutivi nello sconfiggere l’avversario, la colomba, con la forza. Tale deduzione non tiene conto della circostanza in cui, nell’interazione, fossero presenti due individui falchi, dal momento che la loro predisposizione alla conflittualità può comportare delle potenziali perdite per entrambi. Un ulteriore svantaggio derivante dall’appartenenza alla categoria dei falchi dipende dal fatto che nell’interazione competitiva tra due colombe, quest’ultime declinerebbero il conflitto e quindi i costi derivanti dalla lotta con l’avversario, a vantaggio della condivisione della risorsa essenziale.

Tabella n. 5 – La matrice dei guadagni monetari per il gioco dei falchi e delle colombe
Nell’ambito della popolazione aziendale di riferimento consideriamo gli individui che si relazionano tra di loro, casualmente, in rapporto alle tre tipologie di interazioni: due manager collaborativi – cioè due MC – due manager aggressivi – ossia due MF – e per concludere una combinazione mista di un MF e di un MC. La dinamica evolutiva della popolazione dipende dalla struttura dei payoff in relazione alle differenti interazioni tra gli individui. Possiamo ipotizzare la presenza di risorse di natura finanziaria, nell’es. della tabella n. 5 pari a 18€, che possono essere investite interamente in un singolo progetto o altrimenti in due progetti complementari. In particolare, si possono individuare i seguenti scenari:
- Quando entrano in relazione due MC allora le risorse vengono suddivise in due parti uguali e ogni manager dispone di un ammontare pari a 9€. Le risorse vengono distribuite in modo equo tra le parti nell’ambito del singolo progetto o dei due progetti complementari;
- Quando un manager fortemente aggressivo si confronta con uno collaborativo – un MF con un MC – allora si genera un risultato complessivo, tale per cui, il primo entra in possesso dell’intera cifra pari a 18€ mentre il secondo rinunciando al conflitto resta a zero;
- Per concludere, quando due MF entrano in conflitto tra di loro, l’uno vincerà l’intera posta, pari a 18€, mentre l’avversario risulta pari a zero; nell’ambito di questa interazione conflittuale ogni manager deve sostenere dei costi, dovuti al combattimento convenzionale, per un ammontare di 14€, con un payoff atteso pari a 18-14=4 per il vincitore e un payoff atteso di -14€ per lo sconfitto, al fine di poter realizzare il progetto aziendale. Possiamo considerare che ogni manager potrà prevedere di trovarsi vincitore per la metà delle volte e sconfitto per le altre e quindi in ragione dell’intera popolazione dei falchi, presenti nell’azienda, il guadagno medio per ogni manager derivante da questi scontri sarà pari a 4-14/2= -5€.
Con riferimento alla matrice dei guadagni abbiamo individuato due ipotetici manager, A e B, con la loro struttura dei payoff attesi in relazione alle differenti modalità di interazione tra di loro. Per quanto concerne l’analisi strategica della situazione, rappresentata dal gioco in questione, vogliamo comprendere se i guadagni più elevati saranno in corrispondenza di un approccio competitivo da parte del manager MF, o al contrario, di un approccio collaborativo del MC. A tal fine dobbiamo conoscere la probabilità con cui si verifica ogni tipo di interazione all’interno della matrice dei payoff monetari, e quindi, per semplicità si ipotizza una popolazione inizialmente suddivisa in due parti uguali tra le due categorie. Ne consegue che ogni individuo presente nell’impresa avrà il 50% delle possibilità di interagire con un giocatore che esprime delle preferenze comportamentali aggressive o viceversa cooperative. Possiamo calcolare il rendimento medio per un MF e per MC, formato dalla media ponderata dei suoi due payoff[12]:
Payoff falco = 0,5 × [-5] + 0,5 × [18] = 6,5
Payoff colomba = 0,5 × [0] + 0,5 × [9]= 4,5
L’analisi del presente gioco, come già detto in precedenza, prende spunto dallo studio del biologo evoluzionista J.M. Smith[13] che formalizzò il suo principale contributo alla teoria dei giochi con la cosiddetta strategia stabile evolutiva. In quel lavoro, in un’ottica prevalentemente biologica, si metteva in discussione che nella competizione tra le due categorie, i falchi e le colombe, fossero quest’ultime a rischio di estinzione. È sicuramente vero che la categoria con una un maggiore disponibilità di risorse sarà in grado di evolversi più rapidamente, e quindi, la sua quota sulla popolazione complessiva tenderà ad aumentare. Infatti, avendo i falchi la possibilità di entrare in possesso di maggiori risorse, la loro presenza sul totale della popolazione aziendale crescerà. A tal proposito ci si interroga su cosa accadrebbe se aumentasse in modo significativo la presenza dei falchi nel campione di riferimento. La risposta sarà interpretata in funzione della popolazione totale e non del singolo individuo. Se assumiamo per ipotesi che gli individui aggressivi rappresentano circa l’80% della popolazione, allora quest’ultimi potrebbe interagire con un proprio simile almeno 4 volte su 5, di conseguenza siamo in grado di calcolare il payoff medio di entrambi gli individui, in particolare il:
Payoff totale falchi = f × [-5] + 1-f × 18 = 0,8 × [-5] + 0,2 × 18 = -0,4
Payoff totale colombe = f × [0] + 1-f × 9 = 0,8 × [0] + 0,2 × 9 = 1,8
dove:
f = quota di falchi presente nella popolazione
1-f = quota delle colombe presente nella popolazione
Dall’analisi dei dati complessivi dell’intera popolazione si evidenzia come il payoff medio dei MF si riduce notevolmente, rispetto a quello delle colombe, quando quest’ultimi rappresentano i 4/5 dell’intera popolazione, di conseguenza inizierà a diminuire la presenza dei MF nella comunità di riferimento. Infatti, inizialmente con un payoff superiore a quello delle colombe la loro presenza aumenterà, in quanto ogni volta che si confrontano con una colomba ne escono vincenti, ma con il tempo si vedranno aumentare gli scontri tra falchi e di conseguenza si registreranno sempre maggiori perdite per costoro. Questo gioco porterà con il tempo ad un equilibrio tra le due parti se i payoff medi dei due giocatori saranno uguali in corrispondenza di una determinata distribuzione delle due categorie di manager all’interno dell’impresa. Infatti, con payoff medi uguali, i due individui tenderanno a concepire una discendenza egualmente numerosa, e di conseguenza le loro rispettive quote nella popolazione totale rimarranno immutate. Dalla visualizzazione del grafico sottostante si può constatare come la condizione di equilibrio, espressione dell’intersezione delle due curve dei payoff medi tra i due manager, presenta una posizione di stabilità: se la quota percentuale dei MF dovesse subire uno scostamento dal valore 0,6 un processo naturale di interazione tra le parti riporterebbe il gioco nel punto di equilibrio iniziale. Se la percentuale dei MF dovesse scendere al disotto del valore di 0,6, dove la curva dei guadagni medi dei MF è sempre maggiore, e al di sopra, di quella dei MC, allora si riscontrerebbe un aumento nella percentuale dei manager falchi. Mentre, dall’altra parte, in seguito ad un aumento della popolazione dei falchi, al di sopra del punto di equilibrio, il payoff medio per i MF risulterebbe inferiore rispetto a quello dei MC, portando inevitabilmente ad una riduzione della percentuale dei MF.
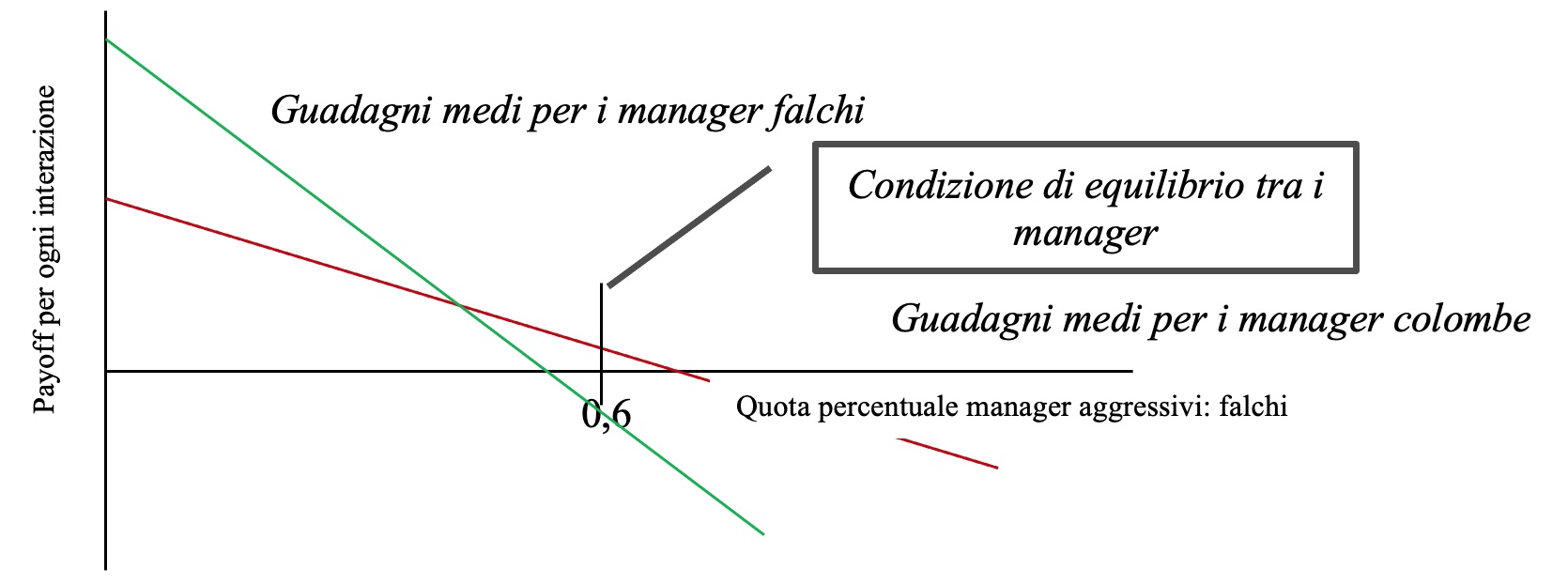
Il gioco in questione mette in rilievo, come l’espressione della preferenza per un determinato comportamento possa dipendere dalla frequenza con cui altri manager nella popolazione condividono tale preferenza. Infatti, investire le proprie preferenze per la strategia aggressiva di un falco può rendere dei vantaggi, ma con un certo limite; quando i manager falchi diventano quantitativamente rilevanti allora risulta più vantaggioso essere una colomba. Come già sottolineato la popolazione dell’impresa presenta una condizione di equilibrio se e solo se i payoff medi per le due preferenze sono uguali.
Considerato il processo dinamico, di interazione tra le parti, che porta alla condizione di equilibrio del gioco siamo in grado di introdurre l’idea di strategia evolutiva stabile, che è quella che permane quando si manifesta una mutazione che cerca di eliminarla. Con la sistematizzazione teorica della suddetta strategia negli studi sull’evoluzione, Smith fu in grado di provare, che tanto una popolazione di soli falchi, quanto una formata solo da colombe non sono evolutivamente stabili e mostrò che, in accordo coi payoff assegnati, una strategia mista con circa il 60% di falchi e il 40% di colombe sarebbe una comunità evolutivamente stabile, ossia protetta di fronte all’incremento di entrambi le parti.
Conclusioni
Il gioco dei falchi e delle colombe evidenzia che nessuna delle due strategie in un’organizzazione è pienamente soddisfacente. Infatti, i MF risultano vincenti nei confronti dei MC, ma perdono nei loro scontri diretti e i MC ottengono un discreto rendimento nel confrontarsi tra di loro, ma non con i MF. Tutto ciò implica che risulterebbe fondamentale l’adozione di un meccanismo di arbitraggio che riduca le lotte tra MF e possa proibire, contemporaneamente, che quest’ultimi possano sfruttare l’atteggiamento cooperativo dei MC, salvando ciò che si ha e riducendo i confronti violenti. In sostanza, l’istituzione dell’arbitraggio viene definito come una strategia “borghese” che sarebbe più stabile e funzionale rispetto alla strategia dei “falchi puri” o delle “colombe pure”. Un manager borghese può agire sia adottando le modalità comportamentali di un falco che di una colomba, a seconda di alcune condizioni ambientali; può scontrarsi, ad esempio, caparbiamente quando incontra un potenziale avversario nel proprio contesto, ma cede quando incontra lo stesso rivale in un altro ambiente. Infatti, i manager borghesi sottopongono il loro conflitto ad un arbitrato esterno per evitare un conflitto prolungato e reciprocamente svantaggioso. Naturalmente la strategia borghese risulta conveniente, a tutte le parti, soprattutto se la situazione si ripete più volte, in modo tale che ogni giocatore può impostare le proprie strategie sulle interazioni precedenti, ponendo la reciprocità come fondamento.
Bibliografia
Ahmand S., Schroeder R.G., “The impact of human resource management practices on operational performance: recognizing country and industry differences”, Elsevier Ltd, 2013.
Arrow K.J., Debreu G., “Existence of an equilibrium for a competitive economy”, in Econometria, 22/3, 1954.
Axelord R., “The evolution of cooperation”, Basic Book, New York, 1984.
Binmore K., “Teoria dei giochi”, Torino, Codice, 2008.
Buonocore F., Ferrara M., “I nuovi contributi: lo Strategic Human Resource Management”, in Ferrara M. (a cura di), La gestione del lavoro flessibile, Giappichelli, 2008.
Casalino N., Saso T., Borin B., Massella E., Lancioni F., “Digital Competences for Civil Servants and Digital Ecosystems for More Effective Working Processes in Public Organizations”, LNCS, Springer, Heidelberg, Germany, 2019.
Casalino N., Cavallari M., De Marco M., Ferrara M., Gatti M., Rossignoli C., “Performance Management and Innovative Human Resource Training through Flexible Production Systems aimed at Enhancing the Competitiveness of SMEs”, IJKM, IUP Journal of Knowledge Management, vol. XIII, No. 4, pp. 29-42, 2015.
Casalino N., Buonocore F., Rossignoli C., Ricciardi F., “Transparency, Openness and Knowledge Sharing for Rebuilding and Strengthening Government Institutions”, in Klement E.P., Borutzky W., Fahringer T., Hamza M.H., Uskov V., Web-based Education, Iasted-Acta Press Zurich, Innsbruck, Austria, 2013.
Casalino N., “Piccole e Medie Imprese e Risorse Umane nell’Era della Globalizzazione”, volume, Collana di Studi di Tecnica Aziendale, n.90, Wolters Kluwer, Cedam, 2012.
Chiarini B., “Un mondo in conflitto. Teoria dei giochi applicata”, Mondadori Università, 2017.
Cicchetti A., “La progettazione organizzativa. Principi, strumenti e applicazioni nelle organizzazioni sanitarie”, Franco Angeli, Milano, 2012.
Colombo F., “Introduzione alla teoria dei giochi”, Roma, Carocci, 2003.
Daft R.L., “Organizzazione Aziendale”, 7 ed., Maggioli Apogeo, 2021.
Frank R.H., “Microeconomics and behavior”, The McGraw-Hill Companies, 2003.
Garfunkel S., “For all practical purposes: introduction to contemporary mathematics”, New York Freeman, 1991.
Gibbons R., “Teoria dei giochi”, Il Mulino, 2005.
Israel G., Millan Gasca A., “Il mondo come gioco matematico. La vita e le idee di John Von Neuman”, Torino, Bollati Boringhieri, 2008.
Jones G.R., “Organizzazione. Teoria, progettazione, cambiamento”, Egea, 2012.
Hegel G.W., “La fenomenologia dello spirito”, Giulio Einaudi editore, Torino, 2008.
Martinez M., Di Nauta P., Sarno D., “Real and apparent changes of organizational processes in the era of big data analytics”, Studi Organizzativi, vol. 2, 2017.
Martinez M., Mangia G., Pezzillo Iacono M., Canonico P., Mercurio R. “The human side of organizational change: Compliance and management control systems in Italian public utilities”, Human Factors and Ergonomics in Manufacturing & Service Industries, vol. 23, p. 47-57, 2013.
Osborne, M.J., “An introduction to game theory”. Oxford University Press, 2004.
Smith J.M., “Evolution and theory of games”, Cambridge University Press, 1982.
Siegfried T., “E’ la matematica, bellezza! John Nash e la teoria dei giochi”, Bollati Boringhieri, 2014.
Simmel G., “The sociology of George Simmel”, Kurt Heinrich Wolff, 1950.
Simon H.A., “A formal Theory of the employment relation”, trad. it. “Causalità, razionalità, organizzazione”, Il Mulino, 1985.
Taylor F., “The principles of scientific management”, Harper & Brothers Publishers, New York and London, 1919.
Von Neuman J., Morgerstern O., “Theory of games and economic behavior”, Princenton University Press, Princeton N.J., 1953.
[1] Secondo la dottrina di Hegel, da intendersi una dialettica di carattere pre-strutturalista, “il conflitto trascende la portata politica e diventa principio metafisico al quale è necessari riferirsi per spiegare la realtà. Nessuna cosa può definirsi se non in relazione a ciò che essa non è”. Vedi Hegel G.W., “La fenomenologia dello spirito”, Giulio Einaudi editore, Torino, 2008.
[2] Taylor F. “The principles of scientific management”, Harper & Brothers Publishers, New York and London, 1919.
[3] Von Neuman J., Morgerstern O., “Theor of games and economic behavior”, Princenton University Press, Princeton N.J., 1953.
[4] Simmel G., “The sociology of George Simmel”, Kurt Heinrich Wolff, 1950.
[5] Si intendono ripetuti quei giochi in cui si ripresenta più volte nel tempo l’interazione fra i giocatori. Molti risultati validi per i giochi che si praticano una volta sola, ad es. il caso del dilemma del prigioniero, non lo sono più in caso di ripetizione, quando i giocatori, interagendo nuovamente, possono reagire alle precedenti strategie degli altri partecipanti.
[6] A. W. Tucker conosciuto per i suoi importanti contributi scientifici nell’ambito della teoria dei giochi, della programmazione non lineare, della topologia. In particolare, nel 1950 diede il nome e la prima interpretazione al più noto ed interessante paradosso della teoria dei giochi, il “dilemma del prigioniero”, che rappresentò un contributo fondamentale al modello di conflitto e cooperazione. In tale gioco due individui, A e B, i quali hanno effettivamente commesso un delitto, sono detenuti in carcere senza poter comunicare tra di loro. Il giudice presenta delle prove insufficienti e quindi può accusarli solo di un reato minimo, per il quale la pena da scontare risulta essere pari ad un anno. Ad ognuno dei due individui viene fatto presente che, se confessasse il delitto più grave, sarebbe messo in libertà, mentre l’altro complice subirebbe una condanna di 10 anni. Se dovessero confessare entrambi, allora pagherebbero con una detenzione pari a 5 anni. Da ciò si evince che in questo gioco la scelta di confessare viene definita una strategia dominante, cioè la strategia che i migliori risultati indipendentemente dalla strategia adottata da parte dell’altro giocatore. Nello specifico indipendentemente dalla scelta di B, l’individuo A riceverà una condanna meno dura confessando la propria colpa. In sostanza se B confessa, allora A subirà 5 anni di detenzione ma se B non confessa, allora A sarà immediatamente libero. Risulta evidente che quando i due giocatori decidono di adottare una strategia competitiva, di massimizzazione dell’interesse personale, entrambi subiranno una perdita di utilità maggiore – 5 anni di detenzione – rispetto alla ricerca di un accordo – 1 anno di detenzione – di collaborazione che fosse reciprocamente vincolato.
| Prigioniero B | |||
|
Prigioniero A |
Confessa | Non confessa | |
| Confessa | 4 anni per ogni prigioniero | 10 anni per A
0 anni per B |
|
| Non confessa | 10 anni per A
0 anni per B |
1 anno per ogni prigioniero | |
Tabella n. 2 – La matrice del gioco il “dilemma del prigioniero”
[7] Axelord R., “The evolution of cooperation”, Basic Book, New York, 1984.
[8] Il biologo evoluzionista J. M. Smith propose, nel suo saggio del 1982 “sull’evoluzione e la teoria dei giochi”, il dilemma noto come falchi e colombe. Quando due animali competono per una preda, generalmente hanno entrambi un’attitudine aggressiva e tentano di vincere l’avversario con l’uso della forza. Quando lo scontro diventa una lotta si presentano due possibilità: quella di abbandonare e fuggire, come nel caso della colomba, abbandonando la preda, ma conservando la vita, oppure combattere, come per i falchi, con un risultato imprevedibile che potrebbe concludersi con la morte.
[9] Smith J.M., “Evolution and theory of games”, Cambridge University Press, 1982.
[10] Per comodità utilizzeremo l’abbreviazione MF per intendere manager falchi per la loro preferenza al comportamento aggressivo.
[11] Per comodità utilizzeremo l’abbreviazione MC per intendere manager colombe per la loro preferenza al comportamento non aggressivo.
[12] Frank R.H., “Microeconomics and behavior”, The McGraw-Hill Companies, 2003.
[13] Smith J.M., “Op. cit.”, Cambridge University Press, 1982

